单独观察屏蔽罩和均压环，选取有代表意义的局部点观察电场强度，见图13、14。在屏蔽罩的拐角处及边缘处选取代表点记录其电场强度值，见表4。在均压环的拐角处及边缘处选取代表点记录其电场强度值，见表5.

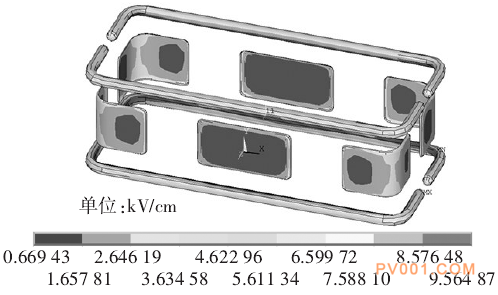
图12考虑金具的屏蔽系统表面电场分布情况

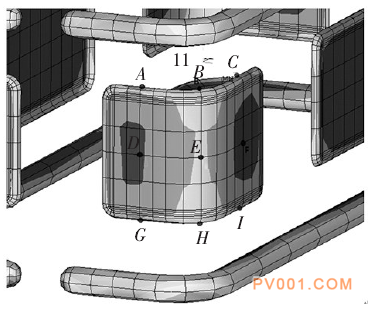
图13选取屏蔽罩局部点

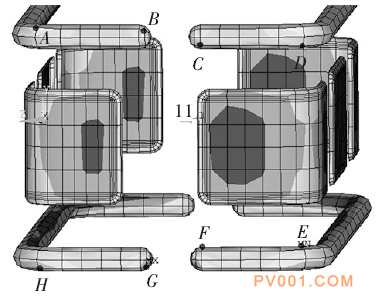
图14选取均压环局部点

4.3 考虑绝缘子的阀塔模型

使用耦合算法可以在考虑绝缘子的影响下计算屏蔽系统的表面电场，通过与无绝缘子模型的对比可以得到绝缘子对屏蔽系统的电场的影响。对有支柱绝缘子的阀塔进行建模，见图15。图15中，在支柱绝缘子的顶部和底部的金具为导体，中间部分为绝缘材料。绝缘子顶部和底部金具和绝缘子是独立划分。为了更方便的处理奇异积分，二者分界面处的剖分完全一致。

在考虑下方支柱绝缘子影响的情况下，给屏蔽罩、均压环、箱体以及上金具加350 kV电位，给下金具施加0 kV电位，其表面电场情况见图16。

表4屏蔽罩局部点电场强度

表5均压环局部点电场强度

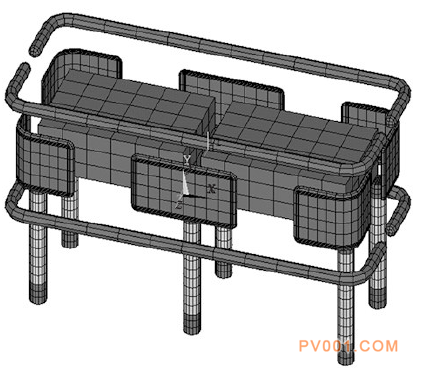
图15考虑支柱绝缘子的阀塔单层

单独观察屏蔽罩和均压环，选取代表性局部点观察电场强度，见图17、18。在屏蔽罩的拐角及边缘处选取代表点记录其电场强度值，见表6；在均压环的拐角及边缘处选取代表点记录其电场强度值，见表7。

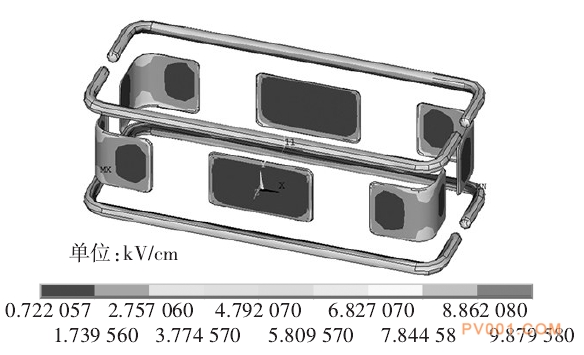
图16考虑绝缘子的屏蔽系统表面电场分布情况

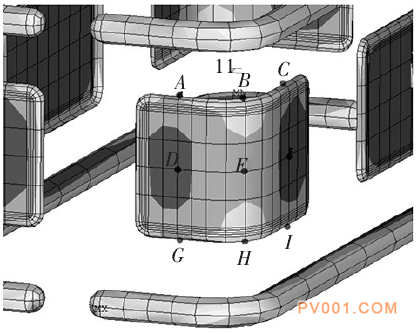
图17选取屏蔽罩局部点

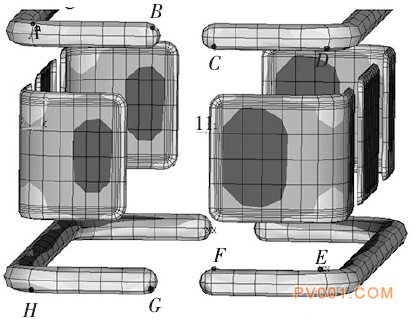
图18选取均压环局部点

表6屏蔽罩局部点电场强度

表7考虑绝缘子情况均压环局部点电场强度

4.4 计算结果对比和误差分析

比较3种情况的屏蔽系统表面电场，见图19。通过图19可以看出，在仿真计算时忽略金具以及绝缘子会使结果明显偏小，尤其是对于靠近绝缘子的屏蔽罩和均压环边缘的电场强度结果影响非常大，不能保证计算结果的正确可靠；对于只考虑金具的屏蔽罩模型的结果，计算精度大幅提高，由于不能考虑绝缘子带来的影响，虽然结果接近准确值，但在靠近绝缘子的屏蔽罩和均压环边缘的电场强度计算结果仍然有较小偏差；使用耦合算法计算考虑绝缘子的屏蔽罩模型，保证了结果的准确性，提高了计算精度，扩展了计算范围。由此可以发现，在计算换流阀屏蔽系统表面电场时不能忽略绝缘子的影响。

图19 3种情况下电场强度对比

4.5 绝缘子内部电场分布

使用耦合算法在计算屏蔽系统表面电场的同时，还可以得到绝缘子内部的电场分布。由于绝缘子对称分布，故分别选取边缘和中间的两个绝缘子中心轴线上的点为路径，绘制绝缘子内部电场强度的变化图，见图20。

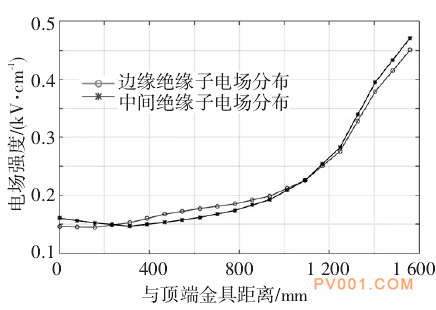
图20 两个绝缘子沿中心线电场强度对比

通过图20可以发现，边缘绝缘子中心线电场强度呈现逐渐上升的趋势，且在绝缘子底部达到最大；中间绝缘子中心线电场强度则呈现先降后升的趋势，其最大值也位于绝缘子底部，且大于边缘绝缘子的场强最大值。

5 结论

1)针对考虑绝缘子的换流阀屏蔽系统，提出了基于积分方程的场域元与边界元耦合的计算方法。通过与二维有限元算法的对比，验证了算法的正确性。

2)通过对有无绝缘子的换流阀屏蔽系统模型的计算结果比较，显示考虑了金具和绝缘子之后，导体表面电场的计算结果会明显增大，靠近绝缘子的屏蔽罩和均压环边缘的电场强度结果变化尤其明显。由此表明在计算换流阀屏蔽系统表面电场时不能忽略绝缘子的影响。

3)通过耦合算法直接计算绝缘子内部的电场强度，发现绝缘子内部场强的分布趋势，在绝缘子底部达到最大。为计算绝缘子内部电场强度提供了一种方法。