2 边界元—场域元耦合算法

2.1 近似函数插值公式

采用四边形单元对导体边界面进行网格划分，在单元上插值，构造表面电位近似函数的表达式为

式(10)中：M₁，M₂，M₃，…，M_n为基函数，在单元上为形状函数；n′n代表整个导体边界面的节点数。

采用六面体单元对电介质区域进行网格划分，在单元上差值，构造电介质电位近似函数的表达式为

式(12)中：M′₁，M′₂，M′₃，…，M′_n为基函数，在单元上为形状函数；n′n代表整个电介质体积内的节点数。

2.2 耦合积分方程的伽辽金离散化

当场点位于导体边界面上时，利用伽辽金加权余量格式对导体表面进行离散，在选取权函数时令其与基函数相同，则式(7)转化为

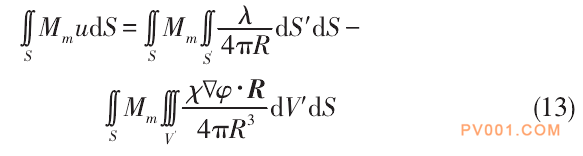
当场点位于介质内部时，利用伽辽金加权余量格式对电介质的体积进行离散，在选取权函数时令其与基函数相同，则式(8)转化为

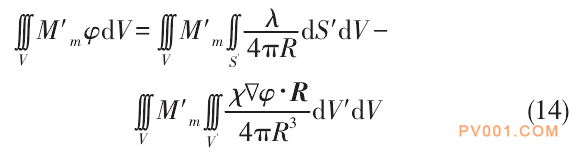
式(14)中：V′表示源区，即源点的积分域；V表示场区，即场点的积分域。由于是求绝缘子内的电位，源点和场点实际上都是待求点，所以式(14)中的V′和V都是电介质的体积。

将式(13)、(14)已知量移到等式右边，未知量移到等式左边，得到：

式(17)中：λ=( λ₁，λ₂，…，λ_n)^T和φ=(φ₁，φ₂，...，φ_n)^T为导体的表面电场和电介质的内电位，是待求量；u=(u₁，u₂，…，u_n)^T为导体的表面电位，是已知量。方程的整体系数矩阵为

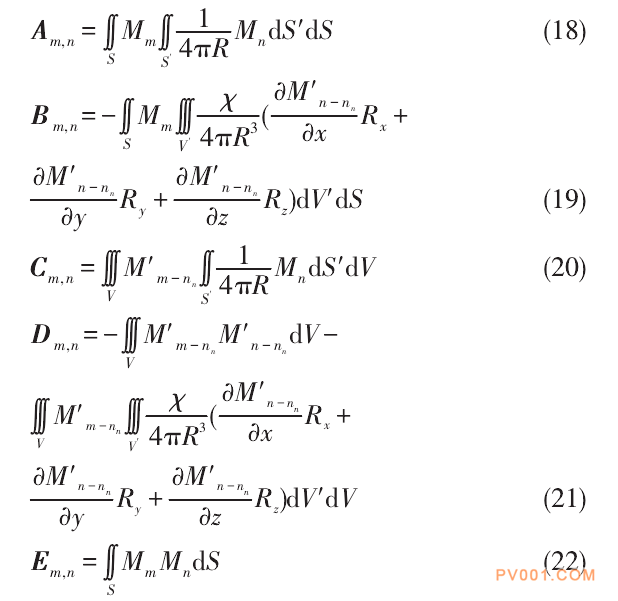
求解方程组(17)即可得到导体表面任意一点的电场和介质内任意一点的电位。

电介质内电场和电位的关系为E=－∇φ，则可根据计算得到的电介质内各点的电位得到电介质内各单元的电场。