流量特性测定

公式1、2和3中的阀门流量系数是按照美国仪表学会标准实践SP39.2，通过实际试验测定的。在1磅/英寸2压降下，流过全开阀门的水的流量（加仑/分钟）定义为流通系数。

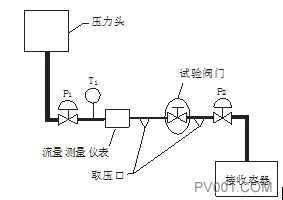
一个代表性的阀门流量试验回路表示在图11[16]中。试验液体通常是温度在40°F和120°F之间的水[17]。有人提议，在整个阀杆行程里每10%的额定流通能力取作测量值。在每种阀门开度下，做出5和20磅/英寸2之间三种压降的试验流量。于是对于每次试验可以根据下面的公式计算出阀门的流量系数，并取计算结果的平均值。

Cv=每分钟通过试验流体的加仑数

由于涡轮流量计精度高，是经常使用的仪表。

在调节回路中的流量特性 最佳的安装流量特性使调节系统能够在受到不同干扰时仍然达到所希望的稳定性、反应速度和精度三项目标。瓦尔期特[10]、齐格勒和尼科尔斯[13]指出，不同的干扰以不同的方式改变过程的静态和动态特性，而这样，每种干扰都可能要求不同的阀门特性。

齐格勒和尼科尔斯通过容器中水温的自动控制论述了过程的各种不同要求。如图12所示，用蒸汽盘管加热容器中的水。

这个过程可以用容器的热平衡简单地表示为：

Mc= qc(T。-T)+qsλ                               

式中 M—容器中水的重量，磅；

C—水的比热，英热单位/磅°F；

T—容器中的水温，°F；

To—流入的水温，°F；

q—水流量，磅/分；

qs—蒸汽流量，磅/分；

λ—蒸汽潜热，英热单位/磅。

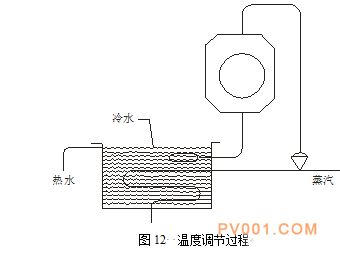
图12 温度调节过程

方程式（4）的左侧表示动态，而其右侧表示容器温度（T）变量之间的关系。在考虑右侧时，那么入口处水温（To）从低负荷（温和的）变到高负荷（冷的）将需要线性变化的蒸汽流量（qs）,于是需要线性流量特性。但是，假若蒸汽供应压力变化，阀门上为临界压力降时的这种关系式应为这种形式：

qs=KCp   

式中 K=常数；

C=在行程X时的阀门流量系数；

P—蒸汔供汽压力，磅/英寸2。

为了保持热平衡中的蒸汽流量（qs）不变，就需要（Cp）保持不变，这就不是线性关系。作者[13]指出，这种使用场合，需要等百分比特性。而对于那种非临界的流动情况，可能仍然需要别的关系（特性）。

布朗[12]研究过一种用于液体流量控制的“工作”压力流量特性，其定义为“阀门相对开度百分数与保持过程工况恒定所控制的流量之间的关系”。这样，线性工作特性就提供了一个恒定的开环增益。计算机计算的工作特性[12]表明：（a）在具有不同干扰的同一控制回路中要保持一个恒定的开环增益，就需不同的安装流量特性，和（b）当阀门过大和过小时，调节质量变坏。这就要求在相同回路里须有不同的流量特性来补偿不同的干扰，这也就意味着没有可供选择的“最好”的流量特性，所选择的流量特性必须是一种折衷方案,能够适应于全部预期的条件.前面的讨论表明最佳的阀门特性一般是做不到的。选择流量特性的基本实用准则就是能够在调节回路的操作范围内提供恒定的相对稳定性[21]。许多过程和测量元件都显示出随产量或某些有关变量的变化而变化的特性（增益和时间常数）。当把热平衡（公式5）改写成描述温度动态响应的形式时，公式5表示为变化着的特性：

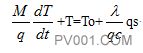
这个时间常数 是导数的系数，并且随着流量变化。蒸汽流量（qs）的系数（增益）随着生产流量变化。这两种与流量有关的变化将改变温度控制系统的相对稳定性。在理论上，能够选择出一种流理特性来补偿这些变化。在这些理想条件下，根据任何负荷条件整定调节器和通过这些整定适应所有操作条件下的动态响应都是可能的。

线性安装流量特性在调节回路中提供恒定阀门增益的价值已经讨论过了。恒定回路相对稳定性的准则在许多情况下都要求一个指定形式的非线性的安装特性。已提出建议，选择恒定开环增益的安装特性是合乎需要的。

开环增益是图13所示的控制回路中全部环节增益的乘积。一种恒定的开环增益导致各种负荷条件下干扰的恒定衰减。巴克里[11]进一步指出，对于动态特性可以忽略不计的过程来说，也即是在图13中Gp=Gr=1的过程，恒定的开环增益将使系统保持恒定的相对稳定性。 

巴克里[11]从恒定数值比率（M）的观点叙述了相对稳定性。在这里，M是被流量与在频率响应技术中心使用基准变量的比率。M—比率是衡量相对稳定性的尺度。液体流量调节系统与测量和控制设备比较而言，其过程动态特性是相对快的。这就意味着，过程动态特性变化对于开环增益没有什么影响。而一个恒定的开环增益导致产生一个恒定的M值和相对稳定。

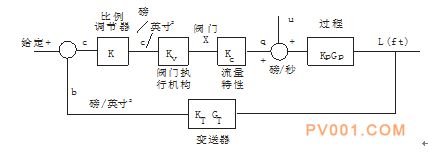
其中 K—调节器增益，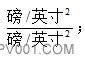

Kv—阀门执行机构增益，；

Kc—流量特性增益，；

Kc—过程增益，

Gp—过程动态特性。

KT—变送器增益，；

GT—变送器动态特性。

调节装置的传递函数为：

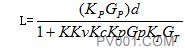
图13 说明开环增益的调节回路

定性。根据图13得：

KKvKcKpKT=KL=常数

式中 KL—开环增益；

Kp—配管增益（对于液体流量过程）；

Kc—固有阀门特性增益

在这里，偏导数是前面定义的阀门增益或灵敏度的比较普通的表示形式。于是，阀门安装特性可以写成：

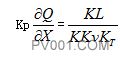
以一次元件例如孔板的平方法则关系代替KT得到下面的阀门安装特性

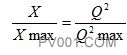
在生产流量变化时，于是需要一个平方根的安装流量特性，以便提供恒定相对稳定性。

那么，把X、Q、△P及对应的C列表可以得到这种固有特性，而且在恒定压降（△P）下，一条X与Q的关系曲线便是这种固有的特性。

后来，巴克里[22]用数字证明了在前面的流量调节系统中，使用传统的线性和等百分比流量特性所产生的相对稳定性的变化。而且，深刻说明方程（8）所表示的平方根特性的优点。

表1列出的调节器增益适合于具有孔板为一次流量元件的流量调节系统。此增益适合恒定的相对稳定性（Mp=2db）。左边的标题栏表明流量是按流量计最大读数的百分数来表示的。

因此，恒定的相对稳定性将要求调节器的比例带对于每种生产流量都要有大的变化。彭伯顿[23]指出，以数字计算机作为调节系统的一部分，代表了一种更为有效的应用方式，对阀门—过程—测量特性产生影响来提供满意的控制性能。如果知道这个安装流量特性合理可靠，可以引用按照公式准确计算的补偿作用，使调节阀与过程匹配适当。可以把方程（1）转换为下面的线性阀门安装特性公式：

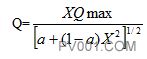
表1 改变流量调节器的比例带，以保持恒定相对稳定性[22]

于是，通过这个偏导数可以确定阀门的增益：

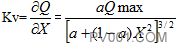
式中

如果采用恒定开环增益准则，则要求的补偿为：

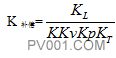
而补偿器的增益为：

式中  C—根据图13的调节器输出。

如果这个调节阀是线性的，而这个过程的增益与流量成反比（如方程6），那么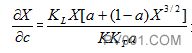，是正确的

而且

与是方程（7）变成：

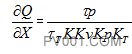
经代入后为：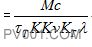

把此式积分。