阀门内流场数值模拟分析研究

彭龑, 郝刘峰

(四川理工学院计算机学院, 四川自贡643000)

摘要:文章在讨论阀门流量系数计算原理的基础上, 给出了阀门内流场数字模拟分析方法。利用COSMOS/FloWorks实现球阀的流量系数计算分析, 计算分析验证了应用CFD技术所计算阀门流量系数的准确性, 并揭示球阀内流场压力的分布情况规律, 为现实的设计生产提出了一种较为简单易行的计算阀门流量系数的方法。

关键词: 阀门;流量系数;流场数值模拟;COSMOS/FloWorks

引言

流场数值模拟也叫流场计算机模拟, 是计算流体力学的核心内容, 也称CFD(ComputationalFluidDynamics) 。它是以计算机为手段, 通过数值计算以数据和图像显示, 再现研究对象及其内在规律。它的兴起促进了实验和理论分析方法的发展, 将实验研究与理论分析方法联系起来, 为简化流动模型的建立提供了更多的依据, 使很多简化方法得到了发展和改善, 利用它研究流体运动的物理特性。

阀门的流量系数是衡量阀门流通能力的指标, 流量系数值越大说明流体流过阀门时的压力损失越小。国外工业发达国家的阀门生产厂家大多把不同压力等级、不同类型和不同公称通径阀门的流量系数值列入产品样本, 供设计部门和使用单位选用。流量系数值随阀门的尺寸、型式和结构而变化, 不同类型和不同规格的阀门都要分别进行试验, 才能确定该阀门的流量系数值。目前, 在我国能够测量阀门流量系数的试验设备很少,远远不能满足实际的需要, 并且这些设备大多是采用传统仪表测量和手动测量的落后方法, 所能达到的精度比较低, 但随着现代CAE技术的发展, 使得这一只能用实验方法测得的数据现在完全可以在虚拟机上通过模拟来实现。

 1 阀门流量系数计算原理

阀门的流量系数是当水流经阀门的两端压差为100kPa时, 某给定行程所流过以m³ /h计的流量数值。

流量系数的计算公式为:

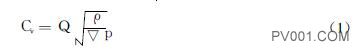
式中, Cv为流量系数m² /3600;Q为流经阀门的流量值,单位为m³ /h;ρ为流体密度, 本系统所用流体为水, ρ=1; p为阀门两端的压力差, 单位为Pa。根据阀门设计的实际情况可知, 一般买家提供给阀门生产厂商的数据都包括管道的压力, 即是阀门的公称压力, 还有管道介质的体积流量。所以要求解阀门的流量系数, 主要工作就集中在对阀门两端的压力差的求解上。由于流体在流动过程中的状态分为层流和紊流, 雷诺系数为其流态的判别数。在工程上, 通常以Re =2320作为临界雷诺数, 即当Re≤2320时, 流态为层流, 当Re≥2320时, 流态为紊流。

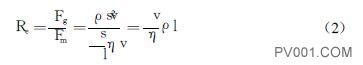
式中, υ为流体的平均速度;L为流束的定型尺寸;η为流体的动力粘度;ρ为流体密度。

根据本文所选实际样本球阀的实际工程应用状况,所分析计算的流体流态为紊流, 分析计算的流体为不可压缩介质, 故这时的标准k-ε模型为:

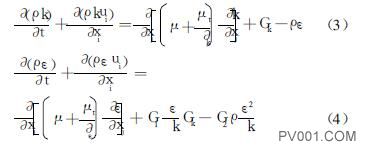
2 阀门内流场数值模拟分析方法

根据流体分析原理和基本方法、阀门内流场的CFD计算任务, 阀门内流场计算机模拟方法如图1所示[ 3-5] 。

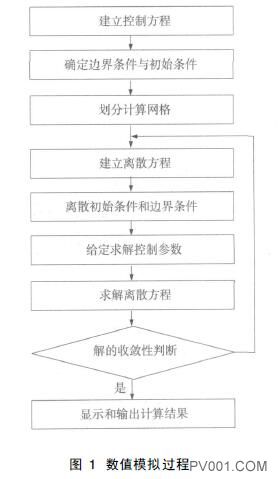
图1 数值模拟过程

(1) 建立控制方程

对于一般的流体流动, 可直接写出其控制方程。对于流动大多是处于湍流范围的流动, 还需要增加湍流方程。

 (2) 确定边界条件与初始条件

控制方程与相应的初始条件、边界条件的组合构成

对一个物理过程完整的数学描述。初始条件是所研究对象在过程开始时刻各个求解变量的空间分布情况。对于瞬态问题, 必须给定初始条件。对于稳态问题, 不需要初始条件。边界条件是在求解区域的边界上所求解的变量或其导数随地点和时间的变化规律, 初始条件和边界条件的处理将直接影响计算结果的精度。

(3) 划分计算网格

对于二维问题, 常用的网格单元有三角形和四边形等形式;对于三维问题, 常用的网格单元有四面体、六面体和三棱体等形式。在整个计算域上, 网格通过节点联系在一起。目前各种CFD软件都配有专用的网格生成工具, 如FLUENT使用GAMBIT作为前处理软件。多数CFD软件可接收采用其他CAD或CFD/FEM软件产生的网格模型。对于问题不是特别复杂时, 可自行编程生成网格。

(4) 建立离散方程

由于所处理的问题自身的复杂性, 一般很难获得方程的真解(或称精确解)。因此, 就需要通过数值方法把计算域内有限数量位置(网格节点或网格中心点)上的因变量值当作基本未知量来处理, 从而建立一组关于这些未知量的代数方程组, 然后通过求解代数方程组来得到这些节点值, 而计算域内其他位置上的值则根据节点位置上的值来确定。由于所引入的应变量在节点之间的分布假设及推导离散化方程的方法不同, 就形成了有限差分法、有限元法和有限元体积法等不同类型的离散化方法。对于瞬态问题, 除了在空间域上的离散外, 还要设计在时间域上的离散后, 使用何种时间积分方案的问题。有限体积法由于其最大限度地保持了差分法的简单性, 又兼有有限元法的精确性, 具有积分守恒性、易于处理边界控制体的特点, 因而目前在二维和三维紊流数值计算中有限体积法得到了广泛而成功的应用。

 (5) 离散初始条件和边界条件

前面所给定的初始条件和边界条件是连续性的, 现在需要针对所生成的网格, 将连续型的初始条件和边界条件转化为特定节点上的值, 这样, 连同各节点处所建立的离散的控制方程, 才能对方程组进行求解。在CFD软件中, 往往在前处理阶段完成了网格划分后, 直接在边界上指定初始条件和边界条件, 然后由前处理软件自动将这些初始条件和边界条件按离散的方式分配到相应的节点上去。

(6) 给定求解控制参数

在离散空间上建立了离散化的代数方程组, 并施加离散化的初始条件和边界条件后, 还需要给定流体的物理参数和湍流模型的经验系数等。此外, 在实际计算时, 还要给定迭代计算的控制精度、瞬态问题的时间步长和输出频率等对计算精度和效率有至关重要的参数量。

(7)求解离散方程

在进行了上述设置后, 生成了具有定解条件的代数方程组。利用数学上已有相应的解法求解, 如线性方程组可采用Gauss消去法或Gauss-Seidel迭代法求解, 而对非线性方程组, 可采用Newton-Raphson方法。在CFD相关软件中, 往往提供多种不同的解法, 以适应不同类型的问题。

(8)判断解的收敛性

对于稳态问题的解, 或是瞬态问题在某个特定时间步上的解, 往往要通过多次迭代才能得到。有时, 因网格形式或网格大小、对流项的离散插值格式等原因, 可能导致解的发散。因此在迭代过程中, 要针对不同的情况对解的收敛性随时进行监视分析, 并在系统达到指定精度后, 结束迭代过程。

(9)显示和输出计算结果

采用线值图、矢量图、等值线图、流线图和云图等方式对计算结果进行说明。