有限单元法——安维士

有限元法简单地说，就是将离散的有限个单元来代替整体的结构，单元的特性由有限个结点上的未知参数来表征，从而实现整体分析部分化、单元化。使用合适的方式，组合包含未知参数的代数方程，这些方程包含各个单元的关系式子组成，利用插值函数，通过所构建的平衡方程组求得节点未知参数，求得插值函数的近似解。以一个单向受拉杆为例，来介绍有限元的计算思想。

如图1所示，拉杆一端固定，另一端受外力P=10kN，拉杆长度L=400mm，横截面积A=100mm2，材料为Q235，，计算轴向变形。

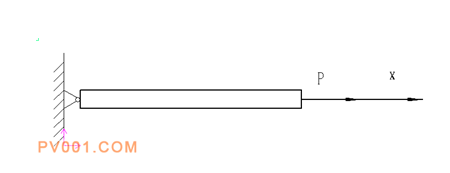
图1根据材料力学胡克定律：

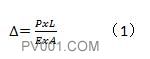
即得图1拉杆右端的位移。将公式1进行简单的移项可改写为公式2

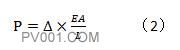
EA/L项即为单元刚度k。

下面开始推导有限元一维杆单元线性静力学典型方程，将图1轴向受拉杆划分成一个杆单元，一个杆单元分左右i、j两个节点，每个节点有一个自由度，即沿X方向的平动自由度。

图2

由图2可知，杆左右两侧均受拉力作用，左侧Pi和右侧Pj的内力由公式2推导如下：

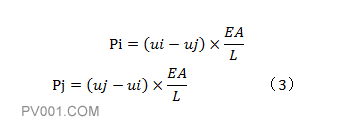
将公式（3）写成矩阵形式

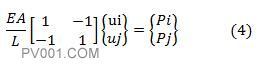
在公式4中有ui和uj两个未知量，若1个节点有1个广义未知量，1个一维杆单元包含两个节点，则1个单元共有两个广义位移未知量，最终构成的矩阵为2X2的方阵。

公式4可简写成公式5

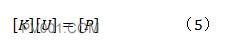
式中，

公式5即为有限元线性静力学的典型方程。

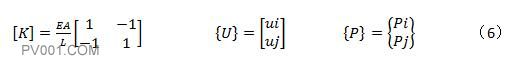
公式4仅为1个单元的静力平衡方程，若将图1的轴向受力构件划分成两个单元，则需要将两个单元平衡方程进行组装。下面就以图1的构件为例，将其划分成两个单元，计算其右侧的轴向位移。

单元划分如图3，左侧定义为1号单元，右侧定义为2号单元，共有 3个节点，3个未知位移，故最终构成的矩阵应该是3X3的方阵。

图3

1号单元的静力平衡方程如公式7：

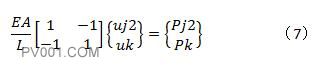
在组装矩阵之前，需要扩充公式6和公式7，扩充矩阵的目的是将3个节点的位移全部纳入到总刚矩阵中便于后面矩阵叠加，扩充后的公式6和公式7如下：

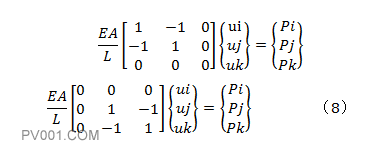
下面将扩充后的公式6和公式7合并、组装，如公式9：

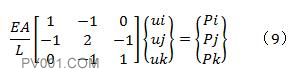
公式9中刚度矩阵K的行列式为0，无法求解图1中杆的位移，因此在使用有限元软件进行静力学分析时，由于结构约束不足，会给出报错提示。

若让式9有解，需要对式9加入边界条件，本例的边界条件是左侧i节点的轴向位移为0，即是已知的，故将式9的第一行和第一列从矩阵中去除，式9变成式10，如下式：

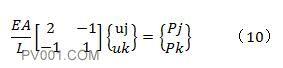
将其它已知条件（弹性模量、杆长、杆截面积及右侧集中力）带入式10：

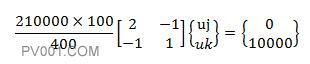
将公式10从矩阵形式改成线性方程组的形式：

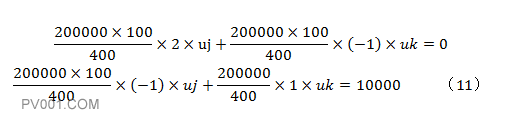
求解公式11，得

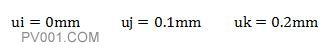
由结果可知，有限元方法求出的基本结果是位移，应变，应力场是基于位移基本解迭代出来的。

作者 李文文 高级工程师

南京安维士传动技术股份有限公司

原标题:有限单元法 | 安维士